Properties of Fractional Division
We are already learnt division of fractional numbers. It is basically multiplication of the first fraction with the reciprocal or multiplicative inverse of another fractional number. In case of finding the multiplicative inverse we actually interchange the numerator and denominators, where a proper fraction is converted into an improper fraction and an improper fraction is converted into a proper fraction. However, this topic deals with the properties of division. The understanding of the properties of division will help the students in better understanding of the concept of division and would lead to more in-depth knowledge along with the properties of multiplication learnt in previous topic as both the properties of division and multiplication are related.
The properties of division of fractional numbers are discussed below:
Property I:
When a fractional number is divided by itself the result is always 1.
Here are few examples to justify property 1:
1. 9/5 ÷ 9/5
= 9/5 × 5/9
= (9 ×5)/(9 ×5)
= 45/45
= 1
2. 15/7 ÷ 15/7
= 15/7 × 7/15
= (15 ×7)/(7 ×15)
= 105/105
= 1
Explanation:
From the examples we can see that any fraction divided by itself is 1. As the fraction is divided by the multiplicative inverse of itself when both the numerator and denominator gets reduced to lowest terms the answer is 1.
Property II:
If a non- zero fractional number is divided by 1 the result is the fractional number itself
Here are few examples to justify property 2:
1. 9/7 ÷ 1
= 9/7 × 1
= 9/7
2. 11/9 ÷ 1
= 11/9 ×1
= 11/9
Explanation:
From the example it is clear that fractional number divided by 1 is the fractional number itself. As the multiplicative inverse of 1 is 1 only. According to the rule of division,
Division = 1st fraction multiplied by the multiplicative inverse of the second fraction/ whole number.
Here the second number is 1 whose multiplicative inverse is also 1. Again according to the properties of multiplication anything multiplied by 1 is the number itself. Hence, fractional number divided by 1 is the fractional number itself.
Property III:
If zero is divided by a non-zero fractional number then the result is zero.
Here are few examples to justify property 3:
1. 0 ÷ 9/5
= 0 × 5/9
= 0
2. 0 ÷ 15/7
= 0 × 7/15
= 0
Explanation:
In the above two examples we can see that when zero is divided by a non-zero fractional number the result is always zero. As we can see that we are finding out the multiplicative inverse of the second fraction. After finding the multiplicative inverse of the second fraction it is actually multiplied with 0 any we know from the properties of multiplication that anything multiplied by zero is zero.
Hence in example (i)
0 ÷ 9/5 = 0
And in example (ii)
0 ÷ 15/7
= 0
Property IV:
As, fractional number cannot be divided by zero hence multiplicative inverse of 0 does not exists.
You might like these
Worksheet on Divisibility Rules | Questions on Test of Divisibility
This is a worksheet which will provide few problems on the divisibility rule of 2, 3, 4, 5, 6, 7, 8, 9, and 10. 1. Check whether the following numbers are divisible by 2 or 3 or both? (i) 2562 (ii) 5693 (iii) 2201 (iv) 7480 (v) 5296 (vi) 4062 (vii) 4568 (viii) 1425 (ix) 1110
Problems on Divisibility Rules | Rules to Test of Divisibility | Test
Here are few problems on the divisibility rules of 2, 3, 4, 5, 6, 7, 8, 9, and 10 which will help the learners in revising their concepts on the divisibility rules. 1. Check whether 3456 is divisible by 2? Solution: The last digit is an even number (i.e. 6) hence 3456 is
Divisible by 10|Test of Divisibility by 10|Rules of Divisibility by 10
The divisibility rule of 10 states that If the last digit of a number is 0 then the given number is divisible by 10. For eg: Check whether 5400 is divisible by 10 or not? Solution: As the last digit of the number is 0 hence, 5400 is divisible by 10
Divisible by 9 | Test of Divisibility by 9 |Rules of Divisibility by 9
This rule states that a number is divisible by 9 if the sum of its digits of the number is divisible by 9 For eg: Check whether 729 is divisible by 9 or not? Sum of the digits = 7 + 2 + 9 = 18 Now 18 is divisible by 9 hence, 729 is also divisible by 9 Here are few examples
Divisible by 8 | Test of Divisibility by 8 |Rules of Divisibility by 8
The most common method to check whether a number is divisible by 8 is to divide and see if the quotient is a whole number or not? If the quotient is a whole number then the given number is divisible by 8. But there is an easier way to check by using the divisibility rule.
Divisible by 7 | Test of Divisibility by 7 |Rules of Divisibility by 7
This rule states that if the difference between twice the digit at units place and the number formed from the remaining digits of the given number is divisible by 7 then the whole number is divisible by 7.
Divisible by 6 | Test of divisibility by 6 |Rules of Divisibility by 6
This topic on divisible by 6 will discuss about the divisibility rule of 6 and few example on the same. Divisibility rule of 6: A number is divisible by 6 if the prime factor of that is 2 & 3 is divisible by 6. For Example: 216 216 is divisible by 2 as the last digit 6 is
Divisible by 5 | Test of divisibility by 5 |Rules of Divisibility by 5
This topic on divisible by 5 will discuss on the divisibility rule of 5 and illustrate few example on the same. Divisibility Rule of 5: If a number ends with 0 or 5 then the number is divisible by 5. For Example: 550 Since the number ends with 0 hence the number is divisible
Divisible by 4 | Rules of Divisibility by 4|Divisibility Rules & Tests
This topic i on divisibility rule of 4 and will provide examples on the same. Divisibility Rule of 4: If the last two digits of the number is divisible by 4 then the whole number is divisible by 4 For eg: 524 The last two digit of the number is 24 which is divisible by 4.
Divisible by 3 | Rules of Divisibility by 3|Divisibility Rules & Tests
This topic is on the divisibility rule of 3 and few examples based on the topic. If the sum of the digits is divisible by 3 then the whole number is divisible by 3. For example 519 The sum of the digits = 5 + 1 + 9 = 15 15 is divisible by 3 hence 519 is also divisible by 3
Divisible by 2 | Divisibility Rule of 2 | Test of Divisibility by 2
This topic would deal with the divisibility rule of 2 and few sums on divisibility rule of 2. Numbers that are ending with 0, 2, 4, 6, and 8 are divisible by 2. That means numbers ending with 0 or multiples of 2 are divisible by 2. We know that numbers which are multiples of
Properties of Divisibility | Divisibility Property |Divisibility Rules
This topic deals with the properties of divisibility which will help us in doing our multiplication and division easy. These rules will help us to determine quickly the factors of certain number, the divisibility criteria of certain number and helps in overall strengthening
Worksheet on Multiples and Factors | List the First Five Multiples
1. List the first five multiples of the following numbers: 2. Choose the numbers that are factors of 24. 3. 3. Choose the numbers that are multiples of 15. 4. Choose the numbers which are multiple of 3 as well as factor of 36
Divisibility Rules | Divisibility Rules from 2 to 12|Divisibility Test
This topic would deal with divisibility rules. There are certain divisibility rules of certain numbers which help in determining that by which number the given number is divisible. Divisibility rules are an effective tool for determining with which numbers a given number
From Properties of Fractional Division to HOME PAGE
Recent Articles
-
Definition of Respiratory Quotient | calculation | Application | Plant
Dec 02, 24 12:09 AM
Definition of respiration quotient- the ratio of the carbon-dioxide evolved to that of the oxygen consumed by a cell, tissue, plants or animals in a given time is called respiratory quotient. It is us… -
Amphibolic Pathway | Definition | Examples | Pentose Phosphate Pathway
Jun 06, 24 10:40 AM
Definition of amphibolic pathway- Amphibolic pathway is a biochemical pathway where anabolism and catabolism are both combined together. Examples of amphibolic pathway- there are different biochemical… -
Respiratory Balance Sheet | TCA Cycle | ATP Consumption Process
Feb 18, 24 01:56 PM
The major component that produced during the photosynthesis is Glucose which is further metabolised by the different metabolic pathways like glycolysis, Krebs cycle, TCA cycle and produces energy whic… -
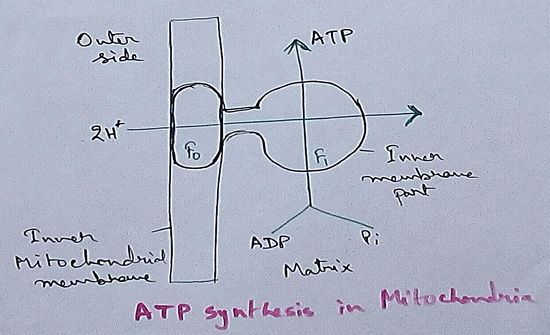
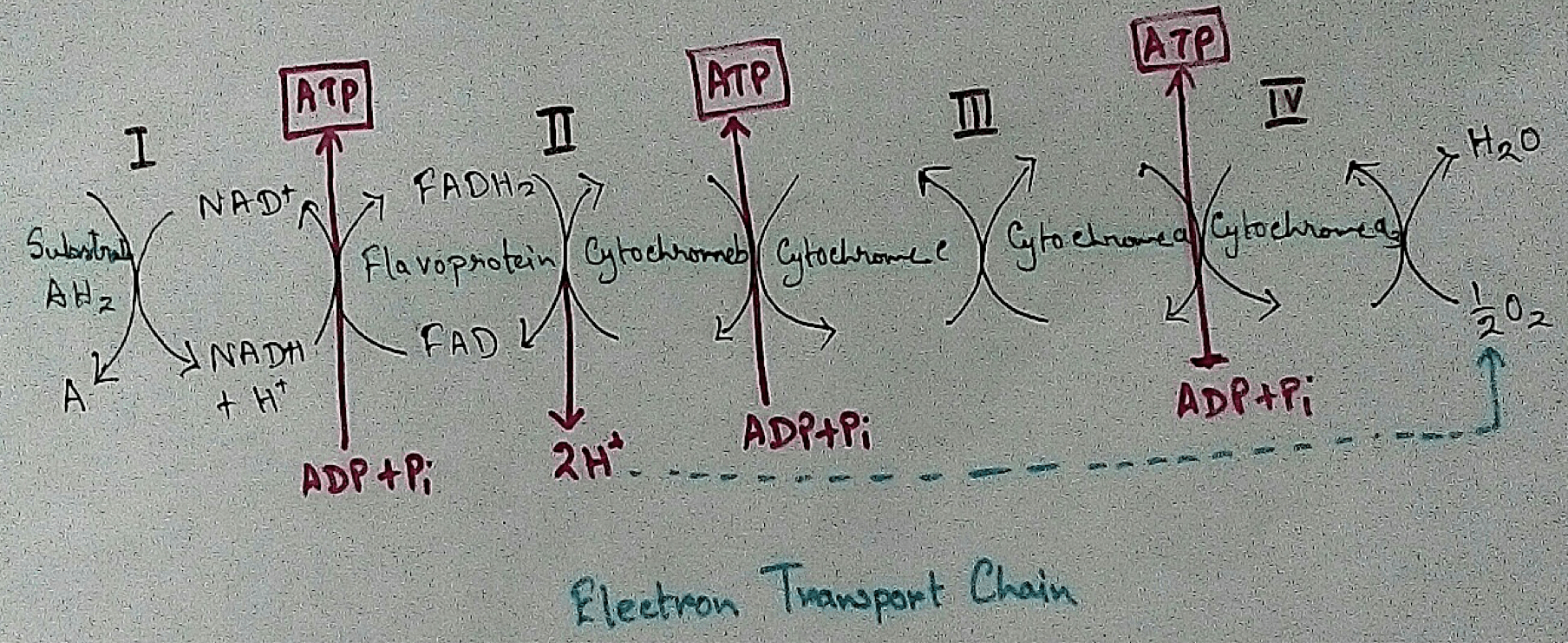
Electron Transport System and Oxidative Phosphorylation | ETC |Diagram
Feb 04, 24 01:57 PM
It is also called ETC. Electron transfer means the process where one electron relocates from one atom to the other atom. Definition of electron transport chain - The biological process where a chains… -
Tricarboxylic Acid Cycle | Krebs Cycle | Steps | End Products |Diagram
Jan 28, 24 12:39 PM
This is a type of process which execute in a cyclical form and final common pathway for oxidation of Carbohydrates fat protein through which acetyl coenzyme a or acetyl CoA is completely oxidised to c…
New! Comments
Have your say about what you just read! Leave me a comment in the box below.