Problems on Multiplication of Fractional Numbers
Here few problems are illustrated on multiplication of fractional numbers. This will give the learners an outline about how story sums on multiplication of fractions are solved. It will also provide the learners a better understanding of application on multiplication of fractional numbers in case of story sums.
1. In a school there are 1500 students. Out of which 3/5 are girls. Find the number of boys.
Solution:
No. of students in a school = 1500
Fraction of girls = 3/5
Number of girls = 3/5 × 1500
= 900
Therefore, no. of boys in the school = 1500 – 900 = 600.
Number of boys in the school = 600 boys
Explanation:
In this problem there are 1500 students. The fraction of girls is mentioned. Hence, it means that ‘of’ 1500 students 3/5 are girls. As we know, that in multiplication ‘of’ means ×. Therefore we will have to multiply 3/5 with 1500 students to find the no. of girls in the school. After getting the no. of girls we can easily find the no. of boys in the school. Since the number of girls in the school is 900 hence, no. of boys in the school will be 1500 – 900 = 600. Therefore there are 600 boys in the school.
2. There are 500 chocolates in a box. Ram distributed 3/4 of the chocolates with his friend. Find the no. of chocolates left in the box.
Solution:
No. of chocolates in a box = 500
Fraction of chocolates Ram distributed = 3/4
Therefore, no. of chocolates distributed by Ram = 3/4 × 500
= 375 chocolates
Therefore, no .of chocolates left in the box = 500 – 375 = 125
No. of chocolates left in the box = 125
Explanation:
There are 500 chocolates in a box. The fraction of chocolates distributed by Ram is mentioned as 3/4 . That means out of 500 chocolates 3/4 is distributed. Therefore we have to multiply 500 with 3/4 to get 375 chocolates. Hence we can easily find no. of chocolates left in the box by subtracting it from 500. So, no. of chocolates left in the box = 500 – 375 = 125 chocolates.
3. There are 450 apples in a basket. 2/5 of the apples are rotten and rest are sold. Find the no. of rotten apples and no. of apples sold.
Solution:
No. of apples in a basket = 450
Fraction of Rotten apples = 2/5
No. of rotten apples = 2/5 × 450
= 180 apples
Therefore, no. of apples sold = 450 – 180
= 270 apples
No. of rotten apples = 180
No. of apples sold = 270
Explanation:
There are 450 apples in a basket. Fraction of rotten apples is mentioned. Hence we can say that 2/5 of 450 apples are rotten. We know that in multiplication ‘of’ means multiply. Hence 2/5 × 450 i.e. 180 apples are rotten. It is mentioned that rest of the apples are sold. Hence 450 – 180 = 270 apples are sold.
You might like these
Worksheet on Divisibility Rules | Questions on Test of Divisibility
This is a worksheet which will provide few problems on the divisibility rule of 2, 3, 4, 5, 6, 7, 8, 9, and 10. 1. Check whether the following numbers are divisible by 2 or 3 or both? (i) 2562 (ii) 5693 (iii) 2201 (iv) 7480 (v) 5296 (vi) 4062 (vii) 4568 (viii) 1425 (ix) 1110
Problems on Divisibility Rules | Rules to Test of Divisibility | Test
Here are few problems on the divisibility rules of 2, 3, 4, 5, 6, 7, 8, 9, and 10 which will help the learners in revising their concepts on the divisibility rules. 1. Check whether 3456 is divisible by 2? Solution: The last digit is an even number (i.e. 6) hence 3456 is
Divisible by 10|Test of Divisibility by 10|Rules of Divisibility by 10
The divisibility rule of 10 states that If the last digit of a number is 0 then the given number is divisible by 10. For eg: Check whether 5400 is divisible by 10 or not? Solution: As the last digit of the number is 0 hence, 5400 is divisible by 10
Divisible by 9 | Test of Divisibility by 9 |Rules of Divisibility by 9
This rule states that a number is divisible by 9 if the sum of its digits of the number is divisible by 9 For eg: Check whether 729 is divisible by 9 or not? Sum of the digits = 7 + 2 + 9 = 18 Now 18 is divisible by 9 hence, 729 is also divisible by 9 Here are few examples
Divisible by 8 | Test of Divisibility by 8 |Rules of Divisibility by 8
The most common method to check whether a number is divisible by 8 is to divide and see if the quotient is a whole number or not? If the quotient is a whole number then the given number is divisible by 8. But there is an easier way to check by using the divisibility rule.
Divisible by 7 | Test of Divisibility by 7 |Rules of Divisibility by 7
This rule states that if the difference between twice the digit at units place and the number formed from the remaining digits of the given number is divisible by 7 then the whole number is divisible by 7.
Divisible by 6 | Test of divisibility by 6 |Rules of Divisibility by 6
This topic on divisible by 6 will discuss about the divisibility rule of 6 and few example on the same. Divisibility rule of 6: A number is divisible by 6 if the prime factor of that is 2 & 3 is divisible by 6. For Example: 216 216 is divisible by 2 as the last digit 6 is
Divisible by 5 | Test of divisibility by 5 |Rules of Divisibility by 5
This topic on divisible by 5 will discuss on the divisibility rule of 5 and illustrate few example on the same. Divisibility Rule of 5: If a number ends with 0 or 5 then the number is divisible by 5. For Example: 550 Since the number ends with 0 hence the number is divisible
Divisible by 4 | Rules of Divisibility by 4|Divisibility Rules & Tests
This topic i on divisibility rule of 4 and will provide examples on the same. Divisibility Rule of 4: If the last two digits of the number is divisible by 4 then the whole number is divisible by 4 For eg: 524 The last two digit of the number is 24 which is divisible by 4.
Divisible by 3 | Rules of Divisibility by 3|Divisibility Rules & Tests
This topic is on the divisibility rule of 3 and few examples based on the topic. If the sum of the digits is divisible by 3 then the whole number is divisible by 3. For example 519 The sum of the digits = 5 + 1 + 9 = 15 15 is divisible by 3 hence 519 is also divisible by 3
Divisible by 2 | Divisibility Rule of 2 | Test of Divisibility by 2
This topic would deal with the divisibility rule of 2 and few sums on divisibility rule of 2. Numbers that are ending with 0, 2, 4, 6, and 8 are divisible by 2. That means numbers ending with 0 or multiples of 2 are divisible by 2. We know that numbers which are multiples of
Properties of Divisibility | Divisibility Property |Divisibility Rules
This topic deals with the properties of divisibility which will help us in doing our multiplication and division easy. These rules will help us to determine quickly the factors of certain number, the divisibility criteria of certain number and helps in overall strengthening
Worksheet on Multiples and Factors | List the First Five Multiples
1. List the first five multiples of the following numbers: 2. Choose the numbers that are factors of 24. 3. 3. Choose the numbers that are multiples of 15. 4. Choose the numbers which are multiple of 3 as well as factor of 36
Divisibility Rules | Divisibility Rules from 2 to 12|Divisibility Test
This topic would deal with divisibility rules. There are certain divisibility rules of certain numbers which help in determining that by which number the given number is divisible. Divisibility rules are an effective tool for determining with which numbers a given number
From Problems on Multiplication of Fractional Numbers to HOME PAGE
Recent Articles
-
Explain about Growth in Plants |Definition of Growth & Differentiation
Feb 27, 25 02:07 PM
Growth is a permanent increase in length or volume of an organism that brought upon by an increase in its dimensions due to synthesis of new protoplasmic material. -
Definition of Respiratory Quotient | calculation | Application | Plant
Dec 02, 24 12:09 AM
Definition of respiration quotient- the ratio of the carbon-dioxide evolved to that of the oxygen consumed by a cell, tissue, plants or animals in a given time is called respiratory quotient. It is us… -
Amphibolic Pathway | Definition | Examples | Pentose Phosphate Pathway
Jun 06, 24 10:40 AM
Definition of amphibolic pathway- Amphibolic pathway is a biochemical pathway where anabolism and catabolism are both combined together. Examples of amphibolic pathway- there are different biochemical… -
Respiratory Balance Sheet | TCA Cycle | ATP Consumption Process
Feb 18, 24 01:56 PM
The major component that produced during the photosynthesis is Glucose which is further metabolised by the different metabolic pathways like glycolysis, Krebs cycle, TCA cycle and produces energy whic… -
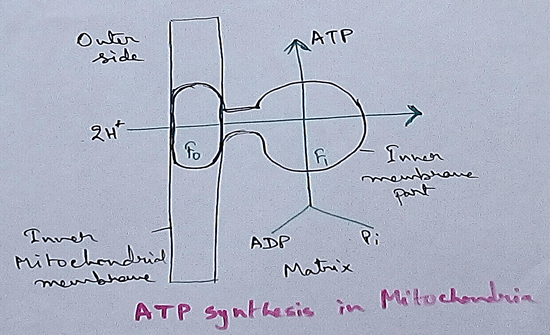
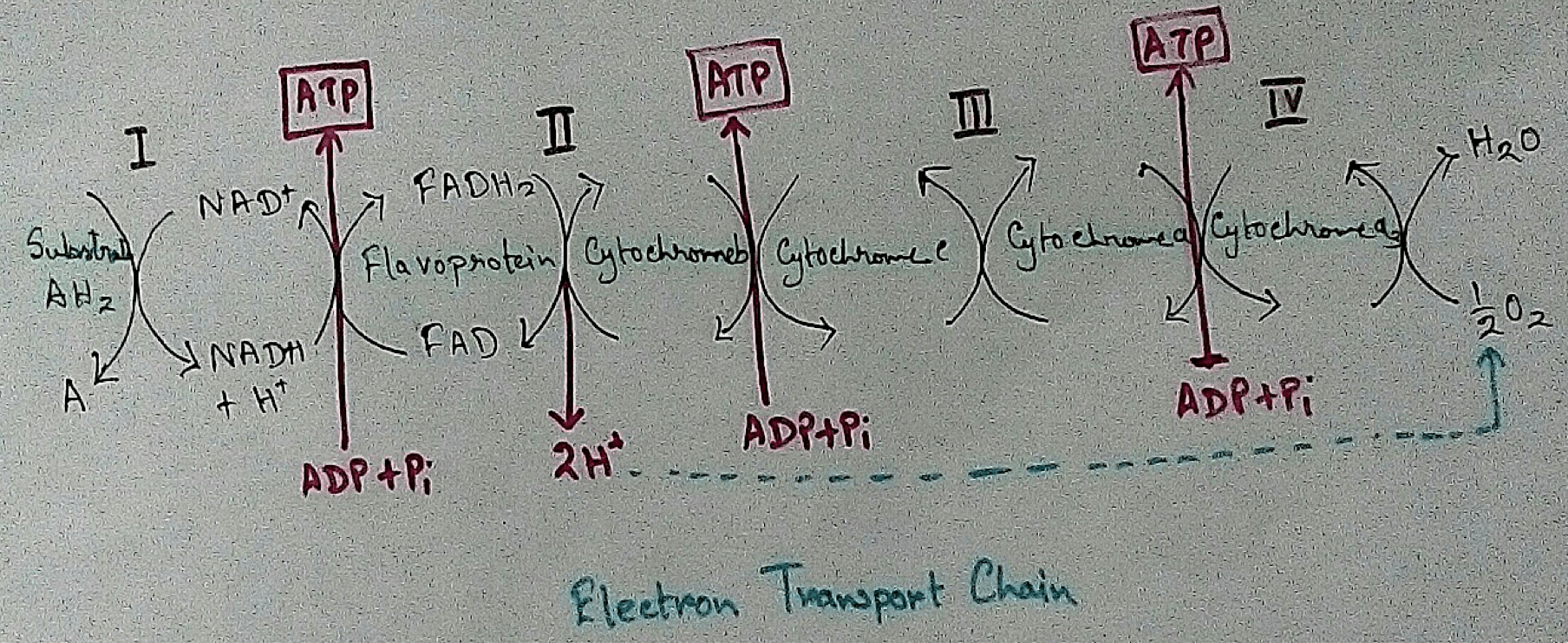
Electron Transport System and Oxidative Phosphorylation | ETC |Diagram
Feb 04, 24 01:57 PM
It is also called ETC. Electron transfer means the process where one electron relocates from one atom to the other atom. Definition of electron transport chain - The biological process where a chains…
New! Comments
Have your say about what you just read! Leave me a comment in the box below.