Subtraction of Whole Numbers

As we have discussed in previous topics whole number is almost same as natural numbers except the fact that it includes zero. However, natural numbers are {1, 2, 3, 4, 5, 6……} whereas whole numbers are {0, 1, 2, 3, 4, 5, 6, 7……}. Hence we can say that all natural numbers are whole numbers but all whole numbers are not natural numbers as it includes zero. Whole numbers are sometimes termed as counting number. However, counting number does not include zero as zero cannot be counted. Therefore counting numbers including zero is termed as whole number.

The four basic operations with whole numbers are addition, subtraction, multiplication, and division. Now we will understand how subtraction of whole numbers is done.

Steps for conducting subtraction of whole numbers:

I. First we have to write the numbers under proper heads of ones, tens, hundreds, thousands, ten thousands……..etc.

II. Then we have to start subtracting from the right hand side. Subtraction can be with borrowing or without borrowing. If borrowing is needed then we have to borrow from the tens column to make adjustment in the ones column. Accordingly if borrowing is needed in the tens column then we will have to borrow from the hundreds column to make adjustment in the tens column and so on and so forth we have to continue likewise.

Solved Examples of Subtraction of Whole Numbers:

2 digit (without borrowing)

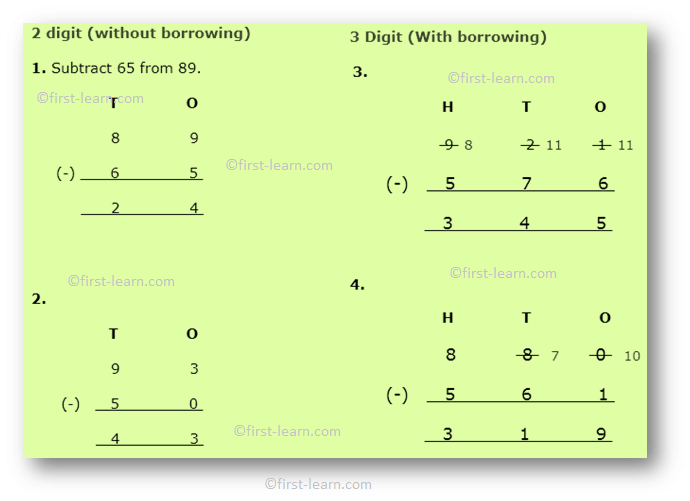
1. Subtract 65 from 89.

                T              O

                8              9

     (-)       6              5 

                2              4 

In ones place 5 is subtracted from 9 to get 4 and in the tens place 6 is subtracted from 8 to get 2.

2.

                T              O

                9              3

      (-)      5              0 

                4              3 

In ones place 0 is subtracted from 3 to get 3 and in tens place 5 is subtracted from 9 to get 4.

3 Digit (Without borrowing)

3.

                H             T              O

                9              8              7

     ( -)      6              5              4 

                3              3              3 

In ones place 4 is subtracted from 7 to get 3 and in tens place 5 is subtracted from 8 to get 3. Similarly 6 is subtracted from 9 to get 3.

4.

                H             T              O

                4              5              6

     (-)       1              2              3 

                3              3              3 

In ones place 3 is subtracted from 6 to get 3 and in tens place 2 is subtracted from 5 to get 3. Similarly 1 is subtracted from 4 to get 3.

3 Digit (With borrowing)

5.

                   H              T             O

                9  8         2  11      1  11

      (-)      5           7           6 

                  3           4           5 

6 cannot be subtracted from 1. Hence 1 is borrowed to make the number in the ones place as 11. So the number in the tens place that is 2 became 1. Now same issue in the tens place that is 7 cannot be subtracted from 1 again. Hence, 1 is borrowed from 9 to make it 8. Now in the tens place after borrowing 7 can be subtracted from 11. Finally in the hundreds place there is no need of borrowing as 5 can be subtracted from 8.

6.

                   H              T              O

                8           8   7      0   10

      (-)      5           6           1 

                  3           1           9 

0 cannot be subtracted from 1. Hence 1 is borrowed to make the number in the ones place as 10. So the number in the tens place that is 8 became 7. Now 6 can be subtracted from 7 in the tens place so no borrowing from the hundreds place required.

The same rule of subtraction with borrowing is prevalent for 4 digit, 5 digit, 6 digit and so on for every number.

From Subtraction of Whole Numbers to HOME PAGE